Chapitre 1. Constructions élémentaires en Python¶

Table des matières¶

1. Introduction

2. Eléments de base

2.1 Variable et affectation
2.2 Types simples (int, bool, float, str) et types composés (tuple, list et dict)

3. Instructions conditionnelles et boucles

3.1 Instructions conditionnelles (si alors sinon)
3.2 Boucle conditionnelle (boucle while)
3.3 Boucle inconditionnelle (boucle for)

4. Fonctions

4.1 Définition d'une fonction
4.2 Espace et portée des variables

5. Spécification des fonctions et tests

5.1 Spécification d'une fonction
5.2 Tests et assertions

Remplissez le jupyter notebook suivant en vous aidant de votre livre de Première NSI de Serge BAYS .

Pour répondre, double-cliquez sur Réponse et complétez la zone en-dessous. Puis cliquez sur le bouton Exécuter.

Important : pour fermer votre jupyter notebook, cliquez sur :

Fichier / Créer une nouvelle sauvegarde

puis sur :

Fichier / Fermer et Arrêter

Ecrivez ci-dessous votre prénom et votre nom :

Réponse :

Chapitre 1. Constructions élémentaires en Python ¶

1. Introduction ¶

Lisez l'introduction du chapitre p. 3

puis répondez dans la zone située sous la question.

Python est un langage de programmation informatique utilisé pour la composition de nombreux logiciels en open source.

Que signifie open source ? (chercher sur le Web).

Réponse :

Point histoire¶

Quelle a été la principale réalisation du scientifique néerlandais né en 1956 Guido van Rossum ?

Réponse :

Lisez le paragraphe Introduction p. 5

puis complétez :

Qu'est-ce qu'un programme informatique ?

Réponse :

Par qui sont écrits les programmes ?

Réponse :

Par qui sont-ils lus ?

Réponse :

Quelle est la version actuelle de Python ?

Réponse :

Python est multiplateforme. Que signifie multiplateforme ?

Réponse :

2. Eléments de base ¶

2.1 Variables et affectation ¶

Lisez le paragraphe Variables et affectation p. 5 et 6

puis complétez :

Si on prend la comparaison d'une variable avec une boite dans laquelle on stocke une donnée, peut-on avoir des noms différents pour une même boite ?

Réponse :

Quel est l'opérateur qui permet d'affecter une donnée à une variable ?

Réponse :

Question avec du code Python

Saisissez dans la fenêtre ci-dessous la triple affectation :
```
x, y, z = 1, 3, 5

print(x, y, z)
```

Enfin cliquez sur le bouton Exécuter. Observez que les nombres 1, 3, 5 ont bien été affectés en une seule ligne à x, y et z.

# Reponse :

Une expression comme 0.5 * x**2 + 1 a-t-elle une valeur ? (en supposant qu'on ait déjà donné une valeur à la variable x)

Réponse :

Quelles sont les différences entre expression et instruction ?

Réponse :

Lisez le paragraphe 1. Convention de style d'écriture de l'Annexe 1

puis complétez :

Comment doit-être écrit votre code ?

Réponse :

Lisez le paragraphe 2. Convention de nommage de l'Annexe 1

puis complétez :

Comment doit-on nommer une constante ? une variable ?

Réponse :

Lisez le paragraphe 3. Commentaires de l'Annexe 1

puis complétez :

Quelles sont les trois façons de commenter un programme écrit en Python ?

Réponse :

Par quel caractère doit commencer tout commentaire en Python afin qu'il ne soit pas pris en compte par l'interpréteur ?

Réponse :

2.2 Types simples (int, bool, float, str) et types composés (tuple, list et dict) ¶

Lisez les paragraphes Types simples et Opérations sur les types numériques p. 6 et haut de la p. 7

puis complétez :

Le type int est utilisé pour représenter quelle sorte de variable ?

Réponse :

Lorsqu'une variable est du type bool (c'est à dire booléen), elle ne peut prendre que deux valeurs. Lesquelles ?

Réponse :

Une variable de type float a une valeur entre $-1.7 \times 10^{308}$ et $1.7 \times 10^{308}$. Vrai ou Faux ?

Réponse :

Lisez le paragraphe Opérations sur les types numériques p.6 et 7 puis complétez :

Question avec du code Python

Saisissez dans la fenêtre ci-dessous un code Python pour calculer :

$$x = {3^{250}}$$

# Reponse :

Division ordinaire

Saisissez dans la fenêtre ci-dessous les lignes de code :
```
a = 4

b = 2

q = a/b

print("q = ", q)
```

Enfin cliquez sur le bouton Exécuter. Observez que la division de deux entiers donne un résultat de type float.

# Reponse :

Comment voyez-vous que q est du type float ?

Réponse :

Saisissez dans la fenêtre ci-dessous la ligne :

print(type(x), type(y), type(q))

Enfin cliquez sur le bouton Exécuter.

# Reponse :

Nous venons de voir que le symbole / est celui de la division non entière (ou tout simplement division). Le quotient $q = {a} \div {b}$ est toujours du type float.

On a toujours $a = b \times q $.

Division euclidienne

Parfois on a besoin de faire une division entière (appelée aussi division euclidienne, du nom du mathématicien Euclide de l'antiquité grecque).

Pour différencier de la division ordinaire, on utilise le symbole // pour obtenir le quotient.

Saisissez dans la fenêtre ci-dessous les lignes de code :
```
a = 4

b = 2

q = a//b

print("q = ", q)
```

Enfin cliquez sur le bouton Exécuter. Observez que la division de deux entiers donne un résultat de type int

# Reponse :

Comment voyez-vous que q est du type int ?

Réponse :

Nous venons de voir que le symbole // est celui de la division entière (ou euclidienne). Le quotient $q $ est toujours du type int.

Si $b$ est un diviseur de $a$, alors le reste $r$ est égal à 0 comme dans l'exemple avec a = 4 et b = 2.

Réponse :

Saisissez dans la fenêtre ci-dessous les lignes de code :

a = 5

b = 2

q = a // b

r = a % b

print("q = ", q)

print("r = ", r)

Enfin cliquez sur le bouton Exécuter. Observez que la division euclidienne donne deux entiers q et r de type int.

# Reponse :

En résumé :

Pour tout couple $(a, b)$ d'entiers naturels, la division euclidienne donne le couple d'entiers naturels $(q, r)$.
// pour obtenir le quotient $q$ dans la division euclidienne.
% pour obtenir le reste $r$ dans la division euclidienne. On dit que % est l'opérateur modulo.

Cas particulier : $$ r = 0 \iff \text{b divise a} $$

Et dans tous les cas : $$ a = bq + r \text{ avec } 0 \leqslant r < b $$

Lisez le paragraphe Comparaison et opérateurs booléens p. 7

puis complétez :

Voici un programme en Python :
```
a = 5

b = 5

a == b
```

Qu'affiche-t-il ?

Réponse :

# Reponse :

Voici un programme en Python :
```
a = 5.0

b = 5

a == b
```

Qu'affiche-t-il ?

Réponse :

# Reponse :

Voici un programme en Python :
```
a = 6

b = 5

a != b
```

Qu'affiche-t-il ?

Réponse :

# Reponse :

Voici un programme en Python :
```
a = False

b = False

a and b
```

Qu'affiche-t-il ?

Réponse :

# Reponse :

Compléter la table suivante :

a	b	a and b
False	False	False
False	True
True	False
True	True

Ce genre de table qui donne la valeur d'une expression logique (c'est à dire avec des and, or, not) est appelée table de vérité.

Voici un programme en Python :
```
a = True

b = False

a or b
```

Qu'affiche-t-il ?

Réponse :

a = True

b = False

a or b

Compléter la table de vérité du or :

a	b	a or b
False	False
False	True
True	False	True
True	True

Voici un programme en Python :
```
a = True

b = not(a)

print(" b = ", b)
```

Qu'affiche-t-il ?

Réponse :

# Reponse :

Compléter la table de vérité du not :

a	not(a)
False
True

Lisez le paragraphe Le type str p. 7

puis complétez :

Le type str est utilisé pour représenter quelle sorte de variable ?

Réponse :

Saisissez dans la fenêtre ci-dessous les lignes de code :

ma_chaine = "Le sapin"

longueur = len(ma_chaine)

print(ma_chaine)

print(longueur)

print(type(ma_chaine))

print(type(longueur))

Enfin cliquez sur le bouton Exécuter.

# Reponse :

L'espace entre Le et sapin est-il compté comme étant un caractère ?

Réponse :

Saisissez dans la fenêtre ci-dessous les lignes de code :

ma_chaine = 'Le sapin'

longueur = len(ma_chaine)

print(ma_chaine)

print(longueur)

Enfin cliquez sur le bouton Exécuter.

# Reponse :

Il n'y a pas de différence entre les guillemets " " et les apostrophes ' '. On peut utiliser aussi bien l'un que l'autre.

Sauf si la chaîne de caractères contient déjà un ce ces symboles.

Par exemple pour L'acacia il y a déjà une apostrophe. Donc on est obligé de mettre cette valeur entre des guillemets.

Saisissez dans la fenêtre ci-dessous les lignes de code :

ma_chaine = "L'acacia"

longueur = len(ma_chaine)

print(ma_chaine)

print(longueur)

Enfin cliquez sur le bouton Exécuter.

# Reponse :

Par exemple pour la chaîne Il dit " Bonjour ! " en entrant. il y a déjà des guillemets. Donc on est obligé de mettre cette valeur entre des apostrophes.

Saisissez dans la fenêtre ci-dessous les lignes de code :

ma_chaine = 'Il dit "Bonjour ! " en entrant.'

longueur = len(ma_chaine)

print(ma_chaine)

print(longueur)

Enfin cliquez sur le bouton Exécuter.

# Reponse :

Soit le code Python suivant :
```
ma_chaine = "L'acacia"
```

Quelle est la valeur de ma_chaine[0] ?

Réponse :

# Reponse :

Soit le code Python suivant :
```
ma_chaine = "L'acacia"
```

Quelle est la valeur de ma_chaine[0:4] ?

Lire le paragraphe 4. Valeurs littérales de l'Annexe 1

puis complétez :

En dehors des valeurs de type nombre entier ou nombre à virgule flottante, chaîne de caractères, True ou False, il existe des variables de valeur None. Qu'est-ce que None signifie ?

Réponse :

Donner un exemple d'instruction qui a la valeur littérale None (c'est à dire Aucune).

# Reponse :

Quel nombre à virgule flottante représente $123.10^{100}$ ?

Réponse :

Quel symbole doit-on mettre au bout d'une ligne de code Python pour signifier que la ligne suivant continue la première ligne sans interruption ?

Réponse :

Lire le paragraphe 5. Opérateurs de l'Annexe 1

puis complétez :

Pourquoi obtient-on 23 lorsqu'on exécute l'expression 3 + 4 * 5 (et non 35) ?

Réponse :

3 + 4 * 5

Que faudrait-il mettre dans l'expression 3 + 4 * 5 pour obtenir 35 ?

Réponse :

(3 + 4) * 5

Pourquoi obtient-on True lorsqu'on exécute l'expression True or False and False (et non False) ?

Réponse :

True or False and False

Que faudrait-il mettre dans l'expression True or False and False pour obtenir False ?

Réponse :

(True or False) and False

Par quels symboles écrit-on le test de différence ?

Réponse :

Par quels symboles écrit-on le test d'égalité ?

Réponse :

Lisez le paragraphe Types composés p. 7

puis complétez :

On a vu précédemment les variables de type simple :

Entier ou integer qui correspondent aux entiers relatifs.
A virgule flottante ou floating point real values qui correspondent aux réels.
Booléen ou Boolean qui correspondent aux valeurs logiques True ou False.
Chaîne ou string qui correspondent aux caractères des textes.

Nous allons maintenant voir quelques types composés qui sont des assemblages de variables de types simples. Nous verrons les types n-uplet, liste, dictionnaire :

N-uplet ou tuple qui sont des groupes non mutables (c'est à dire non modifiables une fois créés) d'entiers, de flottants, de booléens etc. Ils sont notés à la façon des coordonnées, c'est à dire entre parenthèses.

Exemple : mon_tuple = (10, -20, 30.56, 'Vasco de Gama').

Remarque :

Dans un n-uplet, il peut y avoir des éléments de type simple tels qu'entiers, booléens, chaînes de caractères mais aussi des éléments de type composé.

Exemple : mon_tuple_2 = (10, -20, 30.56, 'Vasco de Gama', (3, 9, 0)).

Liste ou list qui sont des groupes mutables (c'est à dire modifiables une fois créés) d'entiers, de flottants, de booléens etc. Ils sont notés entre crochets.

Soit le code Python suivant :

ma_liste = [10, -20, 30.56, 'Vasco de Gama', (3, 9, 0)]

Quelle est la valeur de ma_liste[3] ?

Réponse :

# Reponse :

Quelle est la valeur de ma_liste[1:3] ?

Réponse :

ma_liste = [10, -20, 30.56, 'Vasco de Gama', (3, 9, 0)]
ma_liste[1:3]

Remarque 1 : Les indices de début et de fin - 1

On retrouve la même notation de nommage des éléments pour une liste que pour les chaînes de caractères.

Par exemple ma_chaine[ i : j ] et ma_liste[ i : j ] renvoient les éléments d'indices i inclus à j exclu.

Remarque 2 : Des listes de listes

Comme pour les tuples, on peut trouver dans les listes des éléments de type composé. Par exemple, on peut créer des listes de listes.

On obtient alors un tableau.

Par exemple ma_liste = [['A1', 'A2', 'A3'], ['B1', 'B2', 'B3']] correspond au tableau

A1	B1
A2	B2
A3	B3

Remarque 3 : Modifier une liste déjà existante

Contrairement aux tuples, on peut peut modifier une liste déjà créée, notamment on peut ajouter des éléments à la fin d'une liste déjà existante.

Par la méthode append (ajouter en anglais), on peut par exemple ajouter 'Vasco de Gama' à ma_liste :

Saisissez dans la fenêtre ci-dessous les lignes de code :

ma_liste = [['A1', 'A2', 'A3'], ['B1', 'B2', 'B3']]

longueur = len(ma_liste)

print(ma_liste)

print(longueur)

Enfin cliquez sur le bouton Exécuter.

ma_liste = [['A1', 'A2', 'A3'], ['B1', 'B2', 'B3']]

ma_liste.append('Vasco de Gama')

longueur = len(ma_liste)


print(ma_liste)

print(longueur)

Remarque 4 : Une liste est toujours modifiée sur place

Par la méthode append (ajouter en anglais), on modifie sur place la liste. c'est à dire que l'ancienne liste avant modification n'existe plus.

Si on veut garder une trace de l'ancienne liste, il faut obligatoirement la copier avec par exemple la fonction list().

Saisissez dans la fenêtre ci-dessous les lignes de code :

ma_liste = [['A1', 'A2', 'A3'], ['B1', 'B2', 'B3']]

ma_liste_2 = list(ma_liste)    # Fait une copie dans le but de faire des transformations.

ma_liste_2.append('Vasco de Gama')

print(ma_liste)

print(ma_liste_2)

Enfin cliquez sur le bouton Exécuter.

ma_liste = [['A1', 'A2', 'A3'], ['B1', 'B2', 'B3']]

ma_liste_2 = list(ma_liste)    #  Fait une copie

ma_liste_2.append('Vasco de Gama')

print(ma_liste)

print(ma_liste_2)

Remarque 5 : Une liste spéciale créée avecla fonction range

La fonction range(n) renvoie la suite des entiers partant de 0 jusqu'à n exclu. C'est une variable immutable (du type range).

range() ne renvoie pas une liste.

Pour obtenir automatiquement la liste des entiers de 0 jusqu'à n exclu, il faut utiliser en plus la fonction list()

Ainsi :

  list(range(n))

renvoie la liste [0, 1, 2, ... ,n-1]

Saisissez dans la fenêtre ci-dessous les lignes de code :

ma_liste = list(range(10))

longueur = len(ma_liste)

print(ma_liste)

print(longueur)

Enfin cliquez sur le bouton Exécuter.

ma_liste = list(range(10))

longueur = len(ma_liste)

print(ma_liste)

print(longueur)

Il est possible de ne pas commencer à 0.

Dans ce cas, on précise la valeur de début et la valeur de fin + 1 (rappelez-vous que range(n) renvoie la suite des entiers partant de 0 jusqu'à n exclu).

Saisissez dans la fenêtre ci-dessous les lignes de code :

ma_liste = list(range(2, 10))

longueur = len(ma_liste)

print(ma_liste)

print(longueur)

Enfin cliquez sur le bouton Exécuter.

ma_liste = list(range(2, 10))

longueur = len(ma_liste)

print(ma_liste)

print(longueur)

Enfin, il est possible de préciser le pas de la suite. Par exemple, si on veut les entiers de 2 à 9, en partant de 2 et avec un pas de 3, on précise ce pas en troisième argument.

Saisissez dans la fenêtre ci-dessous les lignes de code :

ma_liste = list(range(2, 10, 3))

longueur = len(ma_liste)

print(ma_liste)

print(longueur)

Enfin cliquez sur le bouton Exécuter.

ma_liste = list(range(2, 10, 3))

longueur = len(ma_liste)

print(ma_liste)

print(longueur)

Comment copier une liste ?¶

Lire le document Copier une liste sur l'Annexe 2

puis complétez :

Cas n°1 : A la fin du programme Python suivant, quelle est la valeur de ma_liste ?
```
ma_liste = [1, 2, 3, 4, 5 ,6]

ma_copie_1 = ma_liste

ma_copie_1[0] = 100
```

Réponse :

ma_liste = [1, 2, 3, 4, 5 ,6]

ma_copie_1 = ma_liste

ma_copie_1[0] = 100

print(ma_liste)

Cas n°2 : A la fin du programme Python suivant, quelle est la valeur de ma_liste ?
```
ma_liste = [[1, 2, 3], [4, 5 ,6]]

ma_copie_1 = ma_liste

ma_copie_1[0][0] = 100
```

Réponse :

ma_liste = [[1, 2, 3], [4, 5 ,6]]

ma_copie_1 = ma_liste

ma_copie_1[0][0] = 100

print(ma_liste)

Cas n°3 : A la fin du programme Python suivant, quelle est la valeur de ma_liste ?
```
ma_liste = [1, 2, 3, 4, 5 ,6]

ma_copie_2 = list(ma_liste)

ma_copie_1[0] = 100
```

Réponse :

ma_liste = [1, 2, 3, 4, 5 ,6]

ma_copie_2 = list(ma_liste)

ma_copie_1[0] = 100

print(ma_liste)

Cas n°4 : A la fin du programme Python suivant, quelle est la valeur de ma_liste ?

ma_liste = [[1, 2, 3], [4, 5 ,6]]

ma_copie_2 = list(ma_liste)

ma_copie_2[0][0] = 100

Réponse :

ma_liste = [[1, 2, 3], [4, 5 ,6]]

ma_copie_2 = list(ma_liste)

ma_copie_2[0][0] = 100

print(ma_liste)

Cas n°5 : A la fin du programme Python suivant, quelle est la valeur de ma_liste ?
```
ma_liste = [1, 2, 3, 4, 5 ,6]

ma_copie_3 = ma_liste[:]

ma_copie_3[0] = 100
```

Réponse :

ma_liste = [1, 2, 3, 4, 5 ,6]

ma_copie_3 = ma_liste[:]

ma_copie_3[0] = 100

print(ma_liste)

Cas n°6 : A la fin du programme Python suivant, quelle est la valeur de ma_liste ?

ma_liste = [[1, 2, 3], [4, 5 ,6]]

ma_copie_3 = ma_liste[:]

ma_copie_3[0][0] = 100

Réponse :

ma_liste = [[1, 2, 3], [4, 5 ,6]]

ma_copie_3 = ma_liste[:]

ma_copie_3[0][0] = 100

print(ma_liste)

Cas n°7 : A la fin du programme Python suivant, quelle est la valeur de ma_liste ?

import copy

ma_liste = [1, 2, 3, 4, 5 ,6]

ma_copie_4 = copy.deepcopy(ma_liste)

ma_copie_4[0] = 100

Réponse :

import copy

ma_liste = [1, 2, 3, 4, 5 ,6]

ma_copie_4 = copy.deepcopy(ma_liste)

ma_copie_4[0] = 100

print(ma_liste)

Cas n°8 : A la fin du programme Python suivant, quelle est la valeur de ma_liste ?

import copy

ma_liste = [[1, 2, 3], [4, 5 ,6]]

ma_copie_4 = copy.deepcopy(ma_liste)

ma_copie_4[0][0] = 100

Réponse :

import copy

ma_liste = [[1, 2, 3], [4, 5 ,6]]

ma_copie_4 = copy.deepcopy(ma_liste)

ma_copie_4[0][0] = 100

print(ma_liste)

En résumé :

Pour copier une liste d'éléments de type simple (int, float, str ou bool) on utilise une copie superficielle par la fonction list ou par nom_de_liste[:].

Pour copier une liste d'éléments de type composé (tuple, list ou dict) on utilise une copie profonde par l'importation de la bibliothèque copy et par la fonction deepcopy de cette bibliothèque.

Lisez le paragraphe Opérations sur les types str et list p. 8

puis complétez :

Dans ce qui suit on considère une variable c de type str ou du type list.

Par exemple on peut avoir c_1 = "L'érable" ou c_2 = [0.28, 4.14, -3e-1]

Appartenance à une chaîne de caractères ou à une liste¶

Quelle est la valeur logique (False ou True) de l'expression "a" in c_1 ?

Réponse :

Vérifiez en exécutant le code Python dans la cellule suivante.

c_1 = "L'érable"

"a" in c_1

Quelle est la valeur logique de l'expression -0.3 in c_2 ?

Réponse :

Vérifiez en exécutant le code Python dans la cellule suivante.

c_2 = [0.28, 4.14, -3e-1]

-0.3 in c_2

indice négatifs = indices en partant de la fin¶

Quelle est la valeur de c_1[-1] ?

Réponse :

Vérifiez en exécutant le code Python dans la cellule suivante.

c_1[-1]

Quelle est la valeur de c_2[-3] ?

Réponse :

Vérifiez en exécutant le code Python dans la cellule suivante.

c_2[-3]

Concaténation de deux chaînes ou de deux listes¶

Saisissez dans la fenêtre ci-dessous les lignes de code :

ma_liste_1 = ['A1', 'A2', 'A3']

mon_supplement = ['A4', 'A5'] 

ma_liste_complete = ma_liste_1 + mon_supplement

print(ma_liste_complete)

Enfin cliquez sur le bouton Exécuter.

ma_liste_1 = ['A1', 'A2', 'A3']

mon_supplement = ['A4', 'A5'] 

ma_liste_complete = ma_liste_1 + mon_supplement

print(ma_liste_complete)

Saisissez dans la fenêtre ci-dessous les lignes de code :

prenom = 'Christophe'

nom_famille = 'Colomb'

nom_complet = prenom + nom_famille

print(nom_complet)

Enfin cliquez sur le bouton Exécuter.

prenom = 'Christophe'

nom_famille = 'Colomb'

nom_complet = prenom + nom_famille

print(nom_complet)

Saisissez dans la fenêtre ci-dessous les lignes de code :

prenom = 'Christophe'

nom_famille = 'Colomb'

nom_complet = prenom + ' ' + nom_famille

print(nom_complet)

Enfin cliquez sur le bouton Exécuter

prenom = 'Christophe'

nom_famille = 'Colomb'

nom_complet = prenom + ' ' + nom_famille

print(nom_complet)

Concaténation de n fois une chaîne ou de n fois une liste¶

Il existe un moyen simple et rapide de produire par exemple 100 fois la chaine de caractères "1". Complétez le code python suivant pour obtenir la chaîne de 100 fois le caractère "1", puis exécutez-le.

rep_unit = 100*"1"

print(rep_unit)

Testez l'opération :

mon_nombre = 3 * rep_unit

print(mon_nombre)

Python considère que rep_unit et du type str.

On voulait que mon_nombre s'écrive avec 100 fois le chiffre 3.

Pour cela on dispose des trois fonctions int() float() str() qui permettent de changer l'argument en un entier ou en un flottant ou en une chaîne.

A l'aide d'une de ces fonctions de conversion, corrigez le code suivant pour que mon_nombre soit égal au nombre qui s'écrit avec 100 chiffres 3.

mon_nombre = 3 * rep_unit

print(mon_nombre)

mon_nombre = 137

ma_chaine = str(mon_nombre)

ma_liste = list (ma_chaine)

print("ma_liste = ", ma_liste)

ma_liste.append('4')

print("ma_liste = ", ma_liste)

nouvelle_chaine = ''.join(ma_liste)

print("nouvelle_chaine", nouvelle_chaine)

Résumons quelques types de variables évoqués ici :¶

Les types simples :

int Entiers
float Booléen
str Chaîne de caractères

Les types composés :

list Listes
tuple N-uplet
dict Dictionnaire

Les types tuple et dict seront étudiés dans d'autres chapitres.

type(a) permet de connaitre le type de la variable a.

Les fonctions de changement de type :

int(a) permet de convertir le type de la variable a en un entier.
float(a) permet de convertir le type de la variable a en un flottant.
str(a) permet de convertir le type de la variable a en une chaîne de caractères.
list(objet) permet de convertir une variable de type str, tuple ou dict en une liste de ses éléments.

mon_flottant = 12.5
ma_chaine = str(mon_flottant)
print(type(ma_chaine))

ma_liste = list(ma_chaine)
print(ma_liste)

Remarque : list(a) fonctionne si et seulement si a est un objet itérable. Une chaîne de caractères est itérable. Mais un flottant n'est pas itérable. C'est pourquoi dans l'exemple ci-dessus nous avons dû d'abord changer grâce à la fonction str() le type de 12.5 de float en str.

Qu'est-ce qu'un objet itérable en Python ? (Faites une recherche sur le Web avec les mots clés itérable et Python).

Réponse :

Trouver un synonyme de itération :

Réponse :

On trouvera sous la forme d'un tableau en annexe 3 le résumé des possibiltés des fonctions de conversion de type selon le type de $a$.
On retiendra qu'on ne peut pas convertir directement un type nombre (int ou float) en un type list ni un type list en un type nombre (int ou float) </p>
On retiendra aussi qu'on peut convertir directement un type chaîne(str) en tout type int, float, list et tout type int, float, list en un type chaîne (str). </p>
Cette dernière propriété fait qu'on passera par l'intermédiaire des chaînes de caractères lorsqu'on veut travailler avec les chiffres d'une nombre.

Exemple :¶

# Calcul de la somme des chiffres d'un entier

mon_nombre = 314
ma_chaine = str(mon_nombre)

somme = 0 # Initialisation de la somme des chiffres a zero.
for i in (ma_chaine):
    print(i)
    chiffre = int(i)  # Il est nécessaire de passer des chaines de caracteres aux entiers,
    somme = somme + chiffre # pour faire la somme.

print("Somme des chiffres = ",somme)

3. Instructions conditionnelles et boucles ¶

En Python, il n'existe pas de "Fin Si", de "Fin Tant que" ni de "Fin Pour".

A la place, on utilise l'indentation qui est un décalage par rapport à la marge.

Quand le décalage est terminé, cela signifie que l'on est sorti du Si ou du Tant que ou du Pour.

If condition est vraie :
    instructions
    ...
    ...
suite du programme

While condition est vraie :
    instructions
    ...
    ...
suite du programme

For i in range():
    instructions
    ...
    ...
suite du programme

L'indentation standard en Python vaut 4 espaces (2 sur les calculatrices TI 83 CE).

Il est pratique d'utiliser la touche Tab de tabulation (grande flèche à gauche du clavier) pour faire automatiquement l'indentation de 4 espaces.

Si on sélectionne à la souris un bloc de plusieurs instructions, la touche Tab permet d'indenter tout le bloc en un seul coup.

Pour supprimer une indentation (c'est à dire faire reculer vers la marge de 4 espaces), on appuie sur la touche Majuscule puis, tout en maintenant la touche majuscule enfoncée, on appuie sur la touche Tab.

Si on sélectionne un bloc d'instructions et qu'on fait Maj + Tab, cela fait reculer le bloc de 4 espaces en un seul coup. Cette méthode est intéressante dès qu'on a des programmes de plusieurs lignes.

3.1 Instructions conditionnelles (si alors sinon) ¶

Dans le paragraphe Instructions conditionnelles et boucles, lisez Instructions conditionnelles p. 8, 9 et 10

puis répondez aux questions suivantes :

Programme 1

On considère un entier $n$ plus grand que zéro.

Complétez, dans la fenêtre ci-dessous, qui effectue les tâches suivantes :

Si $n$ est pair alors on le divise par 2.
Autrement on le multiplie par 3 et on ajoute 1.

n = 3

if n % 2 == 0:

else:

    
print(n)

Remplissez les cellules du tableau suivant :

Valeur de $n$ en entrée	Valeur de $n$ en sortie du programme 1
1	?
2	?
3	?
4	?

Programme 2

On considère un entier $n$ plus grand que zéro.

Ecrivez dans la fenêtre ci-dessous un programme qui effectue les tâches suivantes :

Si $n$ est égal à un multiple de 4 alors on le divise par 4.
Si le reste de la division de $n$ par 4 est égal à 1 alors on affecte à $n$ la valeur de $\frac {3n+1}{4}$.
Si le reste de la division de $n$ par 4 est égal à 2 alors on le divise par 2.
Autrement on affecte à $n$ la valeur de $\frac {3n+1}{2}$.

Remplissez les cellules du tableau suivant :

Valeur de $n$ en entrée	Valeur de $n$ en sortie du programme 2
1	?
2	?
3	?
4	?

3.2 Boucle conditionnelle (boucle while) ¶

Lisez le paragraphe Boucles conditionnelles p. 10

puis répondez aux questions suivantes :

Une boucle conditionnelle commence toujours par le même mot. Lequel ?

Réponse :

Est-il possible qu'une boucle conditionnelle while ne s'arrête jamais ? Si oui, précisez dans quel cas.

Réponse :

Exécutez le programme ci-dessous pour différentes valeurs de $n$. Ecrivez dans le tableau qui suit le temps d'exécution.

Réponse :

n = 1e6  # On mesure le temps d'exécution lorsque n = 1 000 000.
i = 0  #  Initialisation de i.

while i < n:
    i = i + 1
print("boucle terminée !")

Remplissez les cellules du tableau suivant :

Valeur de $n$ en entrée	Durée de la boucle (en s)
$1.10^{6}$	?
$1.10^{7}$	?
$1.10^{8}$	?
$1.10^{9}$	?

Remarque importante :

Lorsque vous écrivez une boucle conditionnelle, vous devez vous assurer que :

La valeur de la condition qui suit le while dépend bien d'au moins une variable qui est modifiée à l'intérieur de la boucle. Sinon la condition aura toujours la valeur True et la boucle est infinie.
Que les modifications successives de la valeur de cette variable conduiront à ce que la condition prenne à un moment la valeur False. Cela permet que la boucle se termine.
La durée totale de la boucle reste raisonnable par rapport au contexte. Par exemple, cela peut être vous-même qui attendez le résultat d'un calcul, d'un dessin etc. ou un système embarqué de pilotage qui attend un résultat avant de donner un ordre à un moteur pour corriger une trajectoire...

3.3 boucle non conditionnelle (boucle for) ¶

Contrairement aux boucles conditionnelles précédentes, on est certain qu'une boucle non conditionnelle se termine puisqu'elle sera exécutée pour le nombre de tours indiqué après le mot-clé for.

Lisez le paragraphe Boucles non conditionnelles p. 10 et 11

puis répondez aux questions suivantes :

Utilisation de la fonction range()¶

Le programme suivant affiche les entiers de 5 à 12. Modifiez-le pour qu'il imprime les entiers de 12 à 5.

for i in range(5, 13):
    print(i)

Utilisation d'une chaîne de caractères¶

Python offre la possibilité de faire une boucle for en utilisant un objet:

  for i in objet:

L'objet doit être une séquence de plusieurs éléments comme une chaîne de caractères ou une liste. On dit que ce sont des objets itérables c'est à dire dont on peut parcourir les valeurs. tuple, dict, set sont d'autres types de variables itérables.

Le programme suivant affiche les caractères de la variable ma_chaine. Modifiez-le pour qu'il affiche chaque caractère 2 fois.

ma_chaine = "L'érable" # Initialisation 

for i in ma_chaine:  #  i est du type str puisque ma_chaine est du type str.
    print(i)

Utilisation d'une liste¶

Voici un programme qui à chaque tour de boucle for ajoute un caractère au bout de la chaine de caractères ma_chaine.

Finalement, à partir d'une liste, on obtient une chaîne de caractères.

ma_liste = ["L", "'", "é", "r", "a", "b", "l", "e"]
longueur = len(ma_liste)

ma_chaine = ""

for i in range(longueur):
    ma_chaine = ma_chaine + ma_liste[i]
    
print (ma_liste)
print (ma_chaine)

En vous aidant de l'exemple précédent, compléter le programme suivant pour qu'il ajoute 4 à chaque élément de la liste ma_liste.

ma_liste = [0, 1, 2, 3]

for i in range(len(ma_liste)):
    ma_liste[i] = 
    
print (ma_liste)

Examinez le code Python suivant. Que fait-il ?

ma_liste=[]  #  Initialisation d'une liste vide
for i in range(10):
    ma_liste.append(2*i)
    print(ma_liste)

Réponse :

# Reponse :

En fin de boucle for, la variable de boucle i conserve la dernière valeur qu'elle avait avant la sortie de boucle. Testez ci-dessous ces programmes :

for i in range(50):
    j = 2*i

print("i = ", i)

puis

for i in "L'érable":
    car = 2*i

print("i = ", i)

4. Fonctions ¶

Les fonctions en Python sont des blocs de programmes placés avant le programme principal qui les appelle.

Par exemple :

  def fonction_1(x):
      .......
      .......
      .......
      return temperature


  def fonction_2(a, b):
      .......
      c = fonction_1(a)
      .......
      return pression


  i, j = 7, 10
  t = fonction_2(i, j)

On voit que le programme principal appelle fonction_2 qui appelle fonction_1.

Les fonctions doivent donc être placées avant le programme principal.

L'intérêt d'utiliser des fonctions est de rendre le code plus compréhensible, particulièrement pour de gros programmes.

4.1 Définition d'une fonction ¶

Lisez le paragraphe Définition d'une fonction p. 12

puis répondez aux questions suivantes :

Par quel mot-clé commence toujours une fonction ?

Réponse :

Ce qu'on appelle arguments d'une fonction sont des variables d'entrée ou de sortie ?

Réponse :

Comment appelle-t-on une fonction qui n'a pas de mot-clé return et donc qui ne retourne rien ?

Réponse :

Voici un exemple de fonction qui prend en argument une liste d'entiers ou de flottants ou le deux et qui renvoie la valeur du plus grand élément de la liste.

def recherche_max(liste):

    """
    Renvoie le plus grand élément de la liste
    Parametres nommes
    -----------------
    liste : de type list
            Cette liste est une liste de nombres du type int ou du type float.

    Retourne
    --------
    max : de type int ou float
          Le plus grand element de la liste.

    """

    max = liste[0]  #  Initialise max avec le premier element de la liste.
    for i in range(len(liste)):
        if liste[i] > max:
            max = liste[i]   #  Actualise la valeur de max

    return max


ma_liste = [12, 8, 11, 3, 19, 20, 17]

print(recherche_max(ma_liste))

En vous basant sur cet exemple, écrivez dans la fenêtre suivante une fonction recherche_min qui prend en argument une liste d'entiers ou de flottants (ou les deux) et qui renvoie le plus petit élément de la liste.

def recherche_min(liste):

    """
    Renvoie le plus petit élément de la liste.
    
    Parametres nommes
    -----------------
    liste : de type list
            Cette liste est une liste de nombres du type int ou du type float.

    Retourne
    --------
    min : de type int ou float
          Le plus petit element de la liste.

    """

    min = liste[0]  #  Initialise max avec le premier element de la liste.
    for i in range(len(liste)):
        if liste[i] < min:
            min = liste[i]   #  Actualise la valeur de min

    return min


ma_liste = [12, 8, 11, 3.14, 19, 20, 17]

print(recherche_min(ma_liste))

Exemple de procédure¶

Voici un exemple de procédure :

def est_premier(n):
    for d in range(2, n): # Teste tous les nombres d de 2 à n-1.
        if n % d == 0 # Teste si d est un diviseur de n.
            compteur = compteur + 1
    if compteur == 0:
        print("n est premier.")
    else:
        print("n n'est pas premier")

On a bien ici une procédure car la fonction est_premier ne renvoie rien. Elle se contente d'afficher si n est premier ou composé.

Pour l'utiliser, on saisira ensuite par exemple :

  est_premier(12)

Recopiez et faites fonctionner dans la fenêtre ci-dessous le code de la procédure est_premier() et tester quelques valeurs de n de votre choix.

def est_premier(n):
    
    compteur = 0  # Initialisation du compteur du nombre de diviseurs
    for d in range(2, n): # Teste tous les nombres d de 2 à n-1.
        if n % d == 0: # Teste si d est un diviseur de n.
            compteur = compteur + 1
            
    if compteur == 0:
        print("n est premier.")  #  n est premier lorsqu'il n'a aucun diviseur de 2 à n-1.
    else:
        print("n n'est pas premier.")

Affichez maintenant la valeur de l'appel de la fonction est_premier(12). Pour cela exécutez dans la fenêtre ci-dessous le code

  print(est_premier(12))

Expliquez les affichages

print(est_premier(12))

4.2 Espace et portée des variables ¶

Lisez le paragraphe Espace et portée des variables p. 13

puis répondez aux questions suivantes :

Soit le programme :

x = 1
def f(x):
    x = x + 1
    return x

print (f(x))
print(x)

Exécutez ce programme. Comment expliquez-vous que print(x) renvoie 1 alors que x a été transformé en x + 1 dans la fonction ?

Soit le programme :

x = 1
def f():
    global x
    x = x + 1
    return x

print(f())
print(x)

Exécutez ce programme. Comment expliquez-vous que cette fois print(x) renvoie 2 alors qu'il renvoyait x = 1 avant ?

En résumé :

Les variables dans les fonctions sont locales. Autrement dit, si une variable a une valeur à l'extérieur d'une fonction, et que cette valeur est modifiée à l'intérieur d'une fonction, cette modification disparait dès qu'on ressort de la fonction. Sauf si on déclare la variable comme global dans le corps de la fonction.

Toutefois, cette méthode n'est pas recommandée car elle peut conduire à des problèmes.

5. Spécification des fonctions et tests ¶

5.1 Spécification d'une fonction ¶

Lisez le paragraphe Spécification d'une fonction p. 13, 14, 15, 16

puis répondez aux questions suivantes :

Une docstring, sorte de notice explicative, est à écrire au début de vos fonctions, juste après la ligne def. D'ailleurs on en a déjà utilisé une précédemment. Voyez ceci :

def recherche_max(liste):

    """
    Renvoie le plus grand élément de la liste.

    Parametres nommes
    -----------------
    liste : de type list
            Cette liste est une liste de nombres du type int ou du type float.

    Retourne
    --------
    max : de type int ou float
          Le plus grand element de la liste.

    """

Remarquez la structure de la docstring en trois parties :

La tâche effectuée par la fonction
les paramètres (ou " arguments ") c'est à dire les valeurs en entrée avec leur types.
Les valeurs retournées avec leur types.

Cette docstring renseigne l'utilisateur sur ce que fait votre fonction. Elle est ouverte par trois $"""$ et est fermée par trois $"""$.

Pour consulter la docstring d'une fonction, il suffit de saisir et d'exécuter le code suivant :

  help(nom_de_la_fonction)

Exécutez dans la cellule suivante le code

  help(recherche_max)

help(recherche_max)

5.2 Tests et assertions ¶

Lisez le paragraphe Tests p. 16, 17

puis répondez aux questions suivantes :

5.2.1 Tester les cas limites ¶

p.14 on a défini la fonction permute

def permute(liste):

    """
    La fonction permute le premier et le dernier élément et renvoie une nouvelle liste.
    permute([1, 2, 3, 4]) renvoie [4, 2, 3, 1]

    Parametres nommes
    -----------------
    liste : de type list

    Retourne
    --------
    copie : de type list

    """

    copie = liste[:]  # Une copie superficielle de la liste.
    copie[0], copie[-1] = copie[-1], copie[0]  # Permutation des éléments d'indice 0 (le premier)
                                           # et d'indice -1 (le dernier).
    return copie

On a écrit une docstring que l'utilisateur peut consulter en saisissant

 help(permute)

help(permute)

On peut faire un test avec une liste de notre choix :

ma_liste = [0, 4, 7, 6, 3]
ma_liste_permutee = permute(ma_liste)

print(ma_liste_permutee)

Mais on doit aussi faire des tests avec des valeurs limites des paramètres.

Sur quel type de listes doit-on encore tester la fonction permute ?

Une liste vide

  ma_liste = []

provoque une erreur.

Ré écrivez ci-dessous la fonction (avec sa docstring) en corrigeant ce problème. On appelera permute_2 la fonction corrigée.

def permute_2(liste):

Testez la fonction permute_2

ma_liste = []

Précédemment, nous avions écrit une fonction pour tester si un entier strictement positif est premier.

def est_premier(n):
    
    compteur = 0  # Initialisation du compteur du nombre de diviseurs
    for d in range(2, n): # Teste tous les nombres d de 2 à n-1.
        if n % d == 0: # Teste si d est un diviseur de n.
            compteur = compteur + 1
            
    if compteur == 0:
        print("n est premier.")  #  n est premier lorsqu'il n'a aucun diviseur de 2 à n-1.
    else:
        print("n est n'est pas premier.")

Cependant, il y a un cas qui n'a pas été traité pour lequel la fonction est_premier renvoie une réponse fausse.

Quel est ce cas ? (Pensez aux cas limites)
Ré écrivez ci-dessous la fonction (avec sa docstring) en corrigeant ce problème. On appellera est_premier_2 la fonction corrigée.

def est_premier_2(n):
    if n == 1:
        print("n n'est pas premier.")
        
    else:
        compteur = 0  # Initialisation du compteur du nombre de diviseurs
        for d in range(2, n): # Teste tous les nombres d de 2 à n-1.
            if n % d == 0: # Teste si d est un diviseur de n.
                compteur = compteur + 1

        if compteur == 0:
            print("n est premier.")  #  n est premier lorsqu'il n'a aucun diviseur de 2 à n-1.
        else:
            print("n n'est pas premier.")

est_premier_2(88095569)

5.2.2 Tester en écrivant des assertions sur des cas variés ¶

Lisez le paragraphe Assertion p.17 à p.21

puis répondez aux questions suivantes :

Une assertion est une affirmation qui peut être True ou False.

En Python, elle s'écrit par exemple :

assert(3 + 2 == 5)

Celle-ci a la valeur True.

En voici une autre qui a la valeur False :

assert(12**2 == 145)

On peut s'en servir pour faire des jeux de tests comme dans l'exemple ci-dessous.

Supposons qu'on ait écrit une fonction addition. Ecrivons une fonction test_addition constituée de tests variés. Ils sont sous forme d'assertions. Si les assertions sont vraies, le test se passe correctement, c'est à dire sans erreur; En fait, il n'arrive rien lorsqu'on exécute la fonction suivie de sa fonction de test.

Exécutez le code dans la cellule ci-dessous :

def addition(a, b):
    s = a + b
    return s

def test_addition():
    assert addition(0, 0) == 0
    assert addition(0, 1) == 1
    assert addition(1, 0) == 1
    assert addition(2, 3) == 5
    assert addition(1.0, 1) == 2.0
    assert addition(1, 2.0) == 3.0
    assert addition(-5, 3) == -2
    
test_addition()

Supposons qu'on ait écrit une erreur dans la fonction addition. Exécutons la fonction addition_2 suivie de la fonction test_addition_2. Remarquez qu'alors s'affiche un message d'erreur qui montre où se trouve la première erreur rencontrée. Ceci doit nous aider à la corriger.

Exécutez le code dans la cellule ci-dessous :

def addition_2(a, b):
    s = a + 0
    return s

def test_addition_2():
    assert addition_2(0, 0) == 0
    assert addition_2(0, 1) == 1
    assert addition_2(1, 0) == 1
    assert addition_2(2, 3) == 5
    assert addition_2(1.0, 1) == 2.0
    assert addition_2(1, 2.0) == 3.0
    assert addition_2(-5, 3) == -2
    
test_addition_2()

5.2.3 Tester sur des exemples dans un premier temps ¶

Exemple de la division euclidienne associe à un couple (a, b)¶

Rappel :

Pour tout couple $(a, b)$ d'entiers naturels avec $b \neq 0$, la division euclidienne donne le couple d'entiers naturels $(q, r)$.
// pour obtenir le quotient $q$ dans la division euclidienne.
% pour obtenir le reste $r$ dans la division euclidienne. On dit que % est l'opérateur modulo.

Cas particulier : $$ r = 0 \iff \text{b divise a} $$

Et dans tous les cas : $$ a = bq + r \text{ avec } 0 \leqslant r < b $$

Le principe de la division d'une valeur a entre b personnes est :

Distribution équitable : Comment distribuer équitablement 30 billes entre 7 personnes ? On donne 1 bille à chacune des 7 personnes. On a alors distribué 7 billes. Il reste 23 billes. On recommence en distribuant encore 1 bille à chacune des 7 personnes. Celles-ci possèdent alors chacune 2 billes et il en reste 16 dans le sac… On continue la distribution tant que le reste est supérieur ou égal au nombre de personnes. Finalement, chaque personne possède 4 billes et il en reste 2 dans le sac.

Une relation vraie avant la boucle, vraie à chaque tour de boucle et vraie après la boucle est un invariant de boucle.

Ici l'invariant de boucle est a = bq + r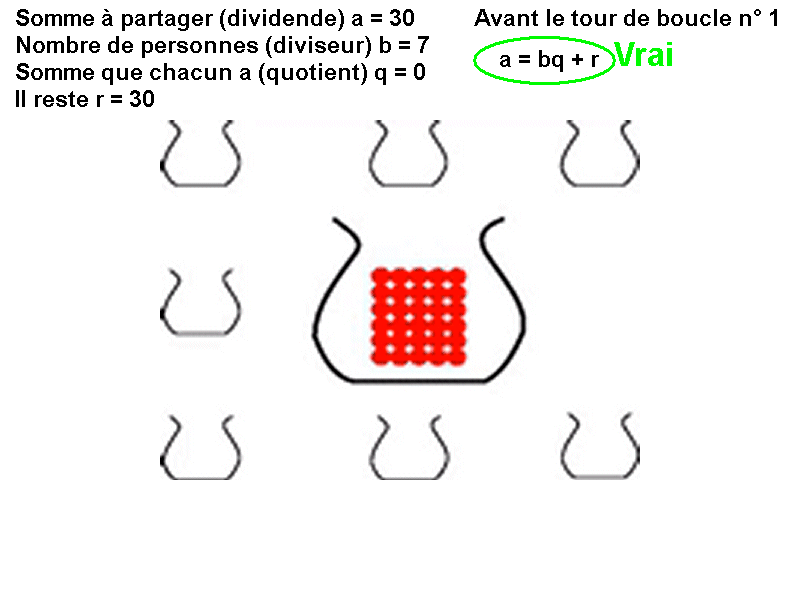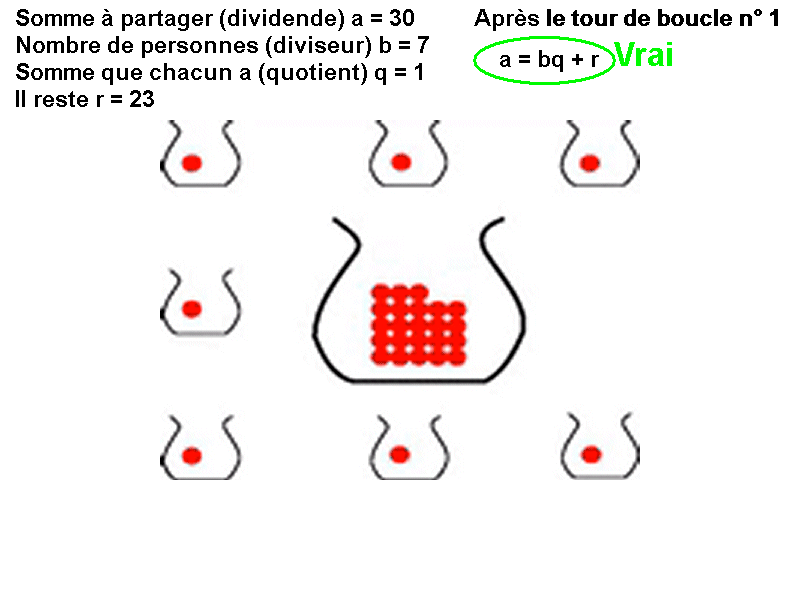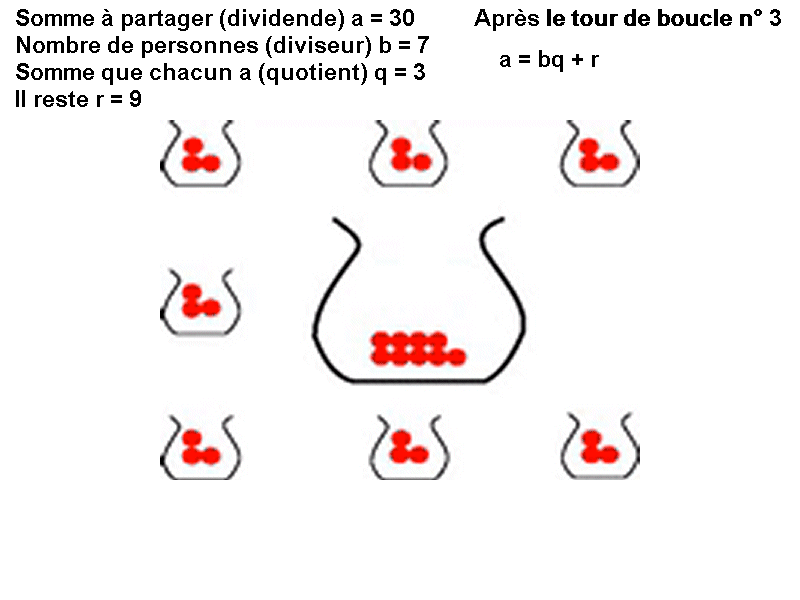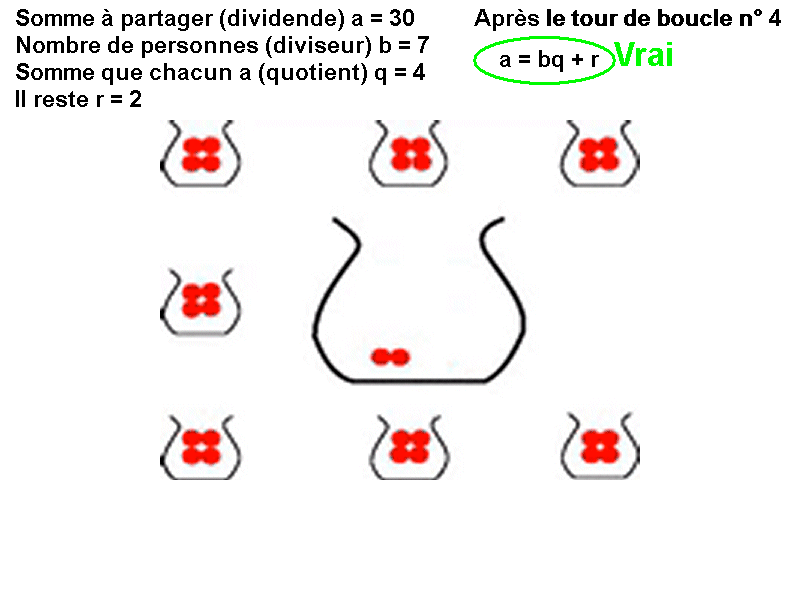

d'où le code de l'algorithme de la division (euclidienne) :

def division (a, b):
    
    """
    La fonction donne le quotient et le reste de la division de a par b.
    division(13, 4) renvoie q = 3 er r = 1.

    Parametres nommes
    -----------------
    a et b : de type int

    Retourne
    --------
    q et r : de type int

    """
    r = a  #  Au depart, a n'a pas ete divise. Donc le reste vaut a et le quotient vaut 0.
    q = 0
    
    while r >= b:  #  On arrete la division quand le reste est plus petit que le diviseur.
        r = r - b  #  A chaque tour, on soustrait le diviseur de ce qui reste,
        q = q + 1  #  et le quotient est augmente de 1.
        
    return q, r

Tester avec un exemple pour voir que le code fonctionne¶

Tout d'abord, faites un test rapide pour vérifier que le programme fonctionne : Saisissez dans la cellule ci-dessous
```
division(30, 7)
```

On sait que la division entière de 30 par 7 donne comme quotient 4 et comme reste 2.

division(30, 7)

Le tuple renvoyé par la fonction correspond au résultat attendu puisque la relation de la division euclidienne $ a = bq + r \text{ avec } 0 \leqslant r < b $ est vérifiée.

En effet on a : $ 30 = 7 \times 4 + 2 \text{ avec } 0 \leqslant 2 < 7 $

Tester sur de nombreux exemples ne suffit pas¶

Tout d'abord nous allons créer une erreur volontaire dans notre algorithme pour voir comment elle peut être détectée.

def division_erreur (a, b):

    """
    La fonction donne le quotient et le reste de la division de a par b.
    division(13, 4) renvoie q = 3 er r = 1.

    Parametres nommes
    -----------------
    a et b : de type int

    Retourne
    --------
    q et r : de type int

    """
    r = a  #  Au depart, a n'a pas ete divise. Donc le reste vaut a et le quotient vaut 0.
    q = 0

    while r > b:  #  On arrete la division quand le reste est plus petit que le diviseur.
        r = r - b  #  A chaque tour, on soustrait le diviseur de ce qui reste,
        q = q + 1  #  et le quotient est augmente de 1.

    return q, r

Où est l'erreur dans ces lignes de code ?

Réponse :

Supposons que vous n'ayez pas vu l'erreur. Tout d'abord, faites un test rapide pour vérifier que le programme fonctionne : Saisissez dans la cellule ci-dessous le programme division_erreur et exécutez-le. Cela permet de le définir pour le noyau en cours de Python.

def division_erreur (a, b):

    """
    La fonction donne le quotient et le reste de la division de a par b.
    division(13, 4) renvoie q = 3 er r = 1.

    Parametres nommes
    -----------------
    a et b : de type int

    Retourne
    --------
    q et r : de type int

    """
    r = a  
    q = 0

    while r > b:  #  Erreur sur la condition de maintien dans la boucle while.
        r = r - b 
        q = q + 1  

    return q, r

Tout d'abord, faites un test rapide pour vérifier que le programme fonctionne : Saisissez dans la cellule ci-dessous
```
print(division_erreur(30, 7))
```

On sait que la division entière de 30 par 7 donne comme quotient 4 et comme reste 2.

division_erreur(30, 7)

Le programme fonctionne sur un exemple. Mais un exemple ce n'est pas beaucoup. On va le faire fonctionner sur beaucoup plus d'exemples.

On va le tester avec tous les couples $(a, b)$ pour $a$ allant de 0 à 12 et $b$ allant de 1 à 12. Cela fera $13 \times 12 = 156$ tests.

Nous utilisons une boucle for imbriquée dans une autre boucle for.

Voyez le programme suivant et exécutez-le :

for a in range(13):
    for b in range(1, 13):
        print(a, b)

On inclut maintenant l'algorithme erroné dans les boucles for imbriquées. Exécutez le code dans la cellule ci-dessous :

for a in range(13):
    for b in range(1, 13):
        print(division_erreur(a, b))

Le code a fonctionné correctement, mais il est difficile de voir s'il y a des erreurs parmi une telle quantité de résultats. On va donc procéder autrement :

5.2.4 Tester par " si not(invariant de boucle) alors return False ¶

On écrit la fonction de test test_division sur le principe précédent des boucles for imbriquées.

Mais au lieu de faire afficher les couples résultats (q, r), on teste si l'invariant de boucle a == b * q + r et r < b est vrai :

Au départ avant la boucle
A chaque tour de boucle

Dans ce cas le test a la valeur logique True

En réalité, on va utiliser la structure de test suivante :

  boucle for sur a:
      boucle for sur b:
          calcul de q, r par la fonction division
          if not(invariant de boucle):
              return False
  return True

On utilise le principe qu'on entre dans le if qu'en cas d'invariant de boucle False.

Mais on ne peut entrer dans un if que lorsque la condition est True.

Donc la condition du if est not(invariant de boucle).

def test_division():
    
    """
    La fonction division renvoie le quotient q et le reste r dans la division de a par b.
    Un invariant est a == b * q + r

    """
    
    for a in range(13):
        for b in range(1, 13):
            q, r = division_erreur(a, b)
            if not(a == b * q + r and r < b): 
                return False  #  Le test est interrompu et retourne False.
    return True  #  Si on n'est jamais rentré dans le if, le test retourne True et s'arrete.

Exécutez la fonction test_division dans la fenêtre ci-dessous. Observez qu'elle renvoie False.

test_division()

On a donc réussi à trouver une erreur. Mais on ne sait pas quand elle se produit.

Une fonction de test plus précise :¶

Il suffit de prévoir, juste avant le return False, de mémoriser les valeurs qu'avaient $a$ et $b$ au moment où l'erreur s'est produite ainsi que les valeurs de $q$ et $r$.

Recopiez le code de la fonction de test en la nommant test_division_2 dans la cellule ci-dessous en y ajoutant les lignes de code qui donneront à l'utilisateur les valeurs des paramètres $a$ et $b$ et des variables de sortie $q$ et $r$ au moment de l'erreur.

def test_division_2():
    
    """
    La fonction division renvoie le quotient q et le reste r dans la division de a par b.
    Un invariant est a == b * q + r

    """
    
    for a in range(13):
        for b in range(1, 13):
            q, r = division_erreur(a, b)
            if not(a == b * q + r and r < b):
                message1 = "Echec pour a = " + str(a) + " et b = " + str(b)
                message2 = "q = " + str(q) + " et r = " + str(r)
                return False, message1, message2
    return True

Exécutez la fonction test_division_2 dans la fenêtre ci-dessous. Observez qu'elle renvoie False.

test_division_2()

Le diagnostic de ce test_division_2 est beaucoup plus précis. Cette fois l'utilisateur peut comprendre que dans l'invariant de boucle, c'est la condition $r < b$ qui n'est pas respectée. Et donc il peut voir où son algorithme a une erreur.

5.2.5 Tester par observation et utilisation des connaissances ¶

Soit les deux fonctions modif1 et modif2 :

def modif1(liste1, liste2):
    
    """
    La fonction modifie liste2 de la facon suivante :
    liste2 contient les memes elements que liste1 s'ils sont positifs ou nuls.
    liste2 contient des 0 aux endroits ou les elements de liste1 sont négatifs.

    Parametres nommes
    -----------------
    liste1 et liste2 : de type int
    
    """
    
    for i in range(len(liste1)):   #  Exploration sur la longueur de la liste1
        if liste1[i] >= 0:
            liste2[i] = liste1[i]
        else :
            liste2[i] = 0

def modif2(liste1, liste2):
    
    """
    La fonction modifie liste2 de la facon suivante :
    liste2 contient les memes elements que liste1 s'ils sont positifs ou nuls.
    liste2 contient des 0 aux endroits ou les elements de liste1 sont négatifs.

    Parametres nommes
    -----------------
    liste1 et liste2 : de type int
    
    """
    
    for i in range(len(liste2)):    #  Exploration sur la longueur de la liste2
        liste2[i] = 0               #  Mise a zero des elements de la liste2
        
    for i in range(len(liste2)):    #  Exploration sur la longueur de la liste2
        if liste1[i] >= 0:
            liste2[i] = liste1[i]

Tout d'abord, faites un test rapide pour vérifier que le programme modif1 fonctionne : Saisissez dans la cellule ci-dessous
```
liste1 = [2, -3, 5, -1]
liste2 = [1, 2, 3, 4]

modif1(liste1, liste2)
print(liste2)
```

On sait que la liste2 devra ressortir modifiée en :

  liste2 = [2, 0, 5, 0]

liste1 = [2, -3, 5, -1]
liste2 = [1, 2, 3, 4]

modif1(liste1, liste2)
print(liste2)

Ensuite, faites un test rapide pour vérifier que le programme modif2 fonctionne : Saisissez dans la cellule ci-dessous
```
liste1 = [2, -3, 5, -1]
liste2 = [1, 2, 3, 4]

modif2(liste1, liste2)
print(liste2)
```

On sait que la liste2 devra ressortir modifiée en :

  liste2 = [2, 0, 5, 0]

liste1 = [2, -3, 5, -1]
liste2 = [1, 2, 3, 4]

modif2(liste1, liste2)
print(liste2)

Conclusion : ce premier test n'a pas réussi à mettre en défaut les codes des fonctions modif1 et modif2.

Une fonction de test qui tient compte du fait que l'on utilise la notation liste[i]¶

Testez le programme modif1 dans le cas particulier où liste2 = liste1. On sait que dans ce cas, il n'y a pas de liste2 copiée mais qu'il s'agit de la même liste avec deux noms.
```
liste1 = [2, -3, 5, -1]

modif1(liste1, liste1)
print(liste1)
```

On sait que la liste2 = liste1 (parce que la place du deuxième argument de la fonction est occupée par liste1) et donc liste1 devra ressortir modifiée en :

  liste1 = [2, 0, 5, 0]

liste1 = [2, -3, 5, -1]

modif1(liste1, liste1)
print(liste1)

Le résultat liste1 = [2, 0, 5, 0] est conforme à l'attente. On n'a pas réussi à mettre en défaut le programme modif1.

Testez le programme modif2 dans le cas particulier où liste2 = liste1.
```
liste1 = [2, -3, 5, -1]

modif2(liste1, liste1)
print(liste1)
```

liste1 devra ressortir modifiée en :

  liste1 = [2, 0, 5, 0]

liste1 = [2, -3, 5, -1]

modif2(liste1, liste1)
print(liste1)

Le résultat liste1 = [0, 0, 0, 0] n'est pas conforme à l'attente. On a réussi à mettre en défaut le programme modif2 dans le cas extrême où on le fait fonctionner en passant sur ses deux arguments une seule et même liste.

Pour mieux comprendre pourquoi on obtient [0, 0, 0, 0] avec la fonction modif2, on va utiliser un outil de visualisation de l'exécution d'un code Python.

Ouvrez le site pythontutor.com .
Copiez dedans le code :

def modif2(liste1, liste2):

    """
    La fonction modifie liste2 de la facon suivante :
    liste2 contient les memes elements que liste1 s'ils sont positifs ou nuls.
    liste2 contient des 0 aux endroits ou les elements de liste1 sont négatifs.

    Parametres nommes
    -----------------
    liste1 et liste2 : de type int

    """

    for i in range(len(liste2)):    #  Exploration sur la longueur de la liste2
        liste2[i] = 0               #  Mise a zero des elemnts de la liste2

    for i in range(len(liste2)):    #  Exploration sur la longueur de la liste2
        if liste1[i] >= 0:
            liste2[i] = liste1[i]

liste1 = [2, -3, 5, -1]

modif2(liste1, liste1)
print(liste1)

Dans Python Tutor, choisissez Python 3.6 puis cliquez sur le bouton "Visualize execution".
Cliquez sur le bouton "Forward" pour avancer pas à pas dans l'exécution du programme.
Observez la flèche rouge à gauche qui montre quelle sera la prochaine instruction à être exécutée.

La fenêtre de droite montre le cadre où travaille l'interpréteur Python à telle ou telle instruction.
Ici, on est dans le cadre du programme principal (global).
Ici, on est dans le cadre de la fonction modif2.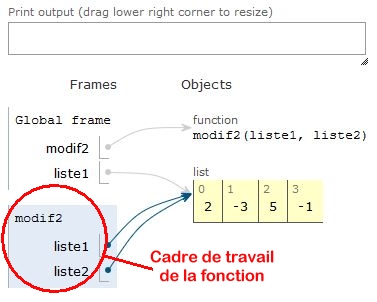

On voit que, dans le cadre de la fonction modif2, liste1 et liste2 sont deux noms d'un seul objet de type list. Donc quand tous les éléments de la liste2 sont initialisés à 0 au début de modif2, les éléments de la liste1 le sont aussi et restent à 0 jusqu'à la fin.
On voit qu'à la dernière étape, quand on revient dans le cadre global, le cadre de la fonction modif2 disparait et la liste1 du cadre global désigne toujours la même liste dont les éléments valent tous 0.